Deterministic Pricing
Overview
Policies can be priced in three ways in ClariNet LS:
- Expectation-based/Probabilistic Pricing: we calculate the expected cashflow using the mortality curve to generate incremental changes in survival probability at each future point in time;
- Stochastic/Monte Carlo Pricing: we use the survival curve to generate a series of dates of death ("trials"). For each trial, the cashflows are projected and we average over all the trials;
- Deterministic Pricing: a single date of death is determined (either based on user input or a known point in time (e.g. coverage end date, Aged LE50 date). The cashflows are projected to this date to determine the policy value.
This document focuses on the various ways of calculating policy results based on Deterministic Pricing.
Deterministic Pricing Parameters
The selection of deterministic pricing parameters from these two dropdowns on the portfolio pricing page:
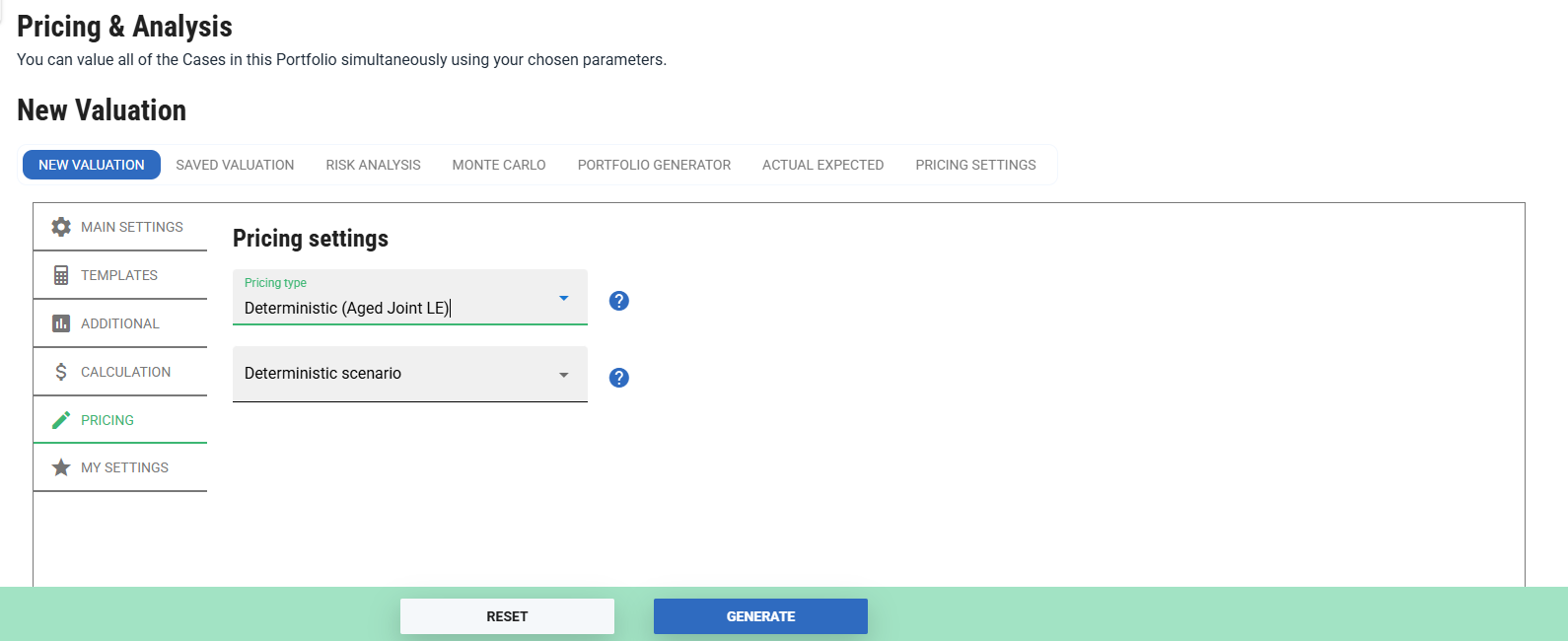
Pricing Type
Pricing Type has three deterministic settings:
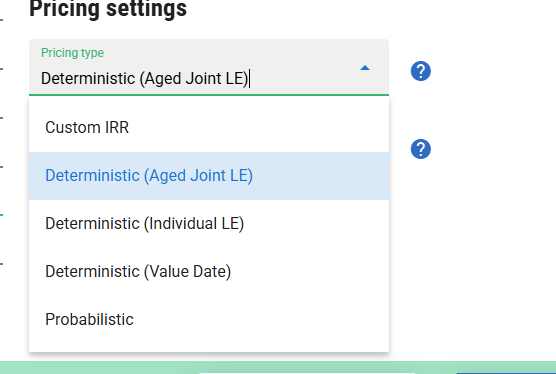
- Deterministic (Aged Joint LE): an aged LE50 is calculated on Value Date (joint if this is a joint life policy) and the date of death is calculated based on Value Date + Aged LE50;
- Deterministic (Individual LE): a date of death is calculated based on the blended underwriting date plus the blended LE50. For a joint life policy, either the earlier or later of these dates is used depending on the joint life payout type. Note that this type of valuation implies “straight aging” and will therefore lead to high valuations;
- Deterministic (Value Date): a date of death is calculated from Value Date plus the bump specified in the Deterministic Scenario drop-down. For example, if value date is 19-June-2019 and we specify LE + 12m, the date of death will be 19-June-2020.
Once a Deterministic setting has been applied, a further drop-down appears:
Deterministic Scenario
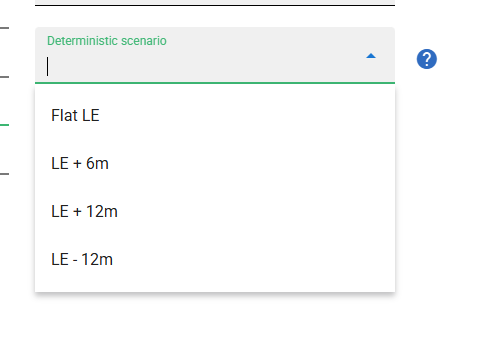
This drop down determines whether the LE50 is used or a specified bump is applied to that LE50. Note that additional bumps can be specified by adding them in Pricing and Risk.
The deterministic scenarios are specified under Pricing and Risk→Determinsitic Pricing Scenarios, where you will find this:
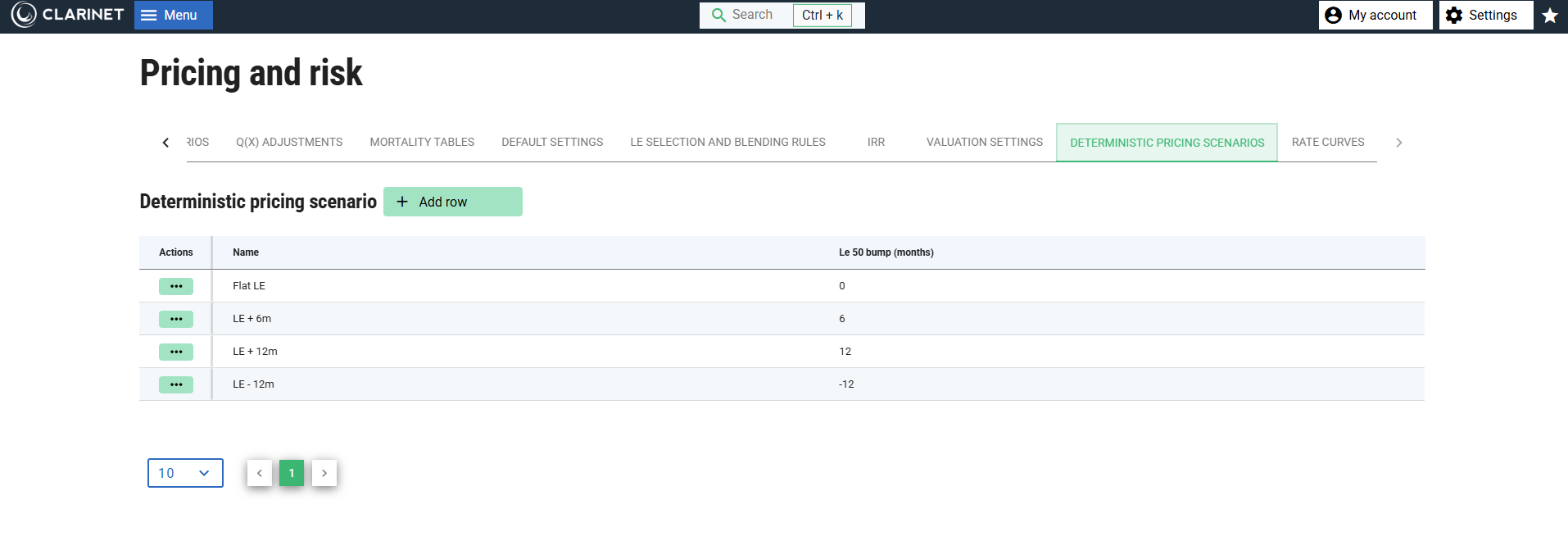
- Based on the bump setting, the meaning of the deterministic scenarios is as follows:
- Deterministic (Aged Joint LE): an aged LE50 is calculated on Value Date (joint if this is a joint life policy) and the date of death is calculated based on Value Date + Aged LE50;
- Deterministic (Individual LE): a date of death is calculated based on the blended underwriting date plus the blended LE50. For a joint life policy, either the earlier or later of these dates is used depending on the joint life payout type;
- Deterministic (Value Date): a date of death is calculated from Value Date plus the bump specified in the Deterministic Scenario drop-down. For example, if value date is 19-June-2019 and we specify LE + 12m, the date of death will be 19-June-2020.
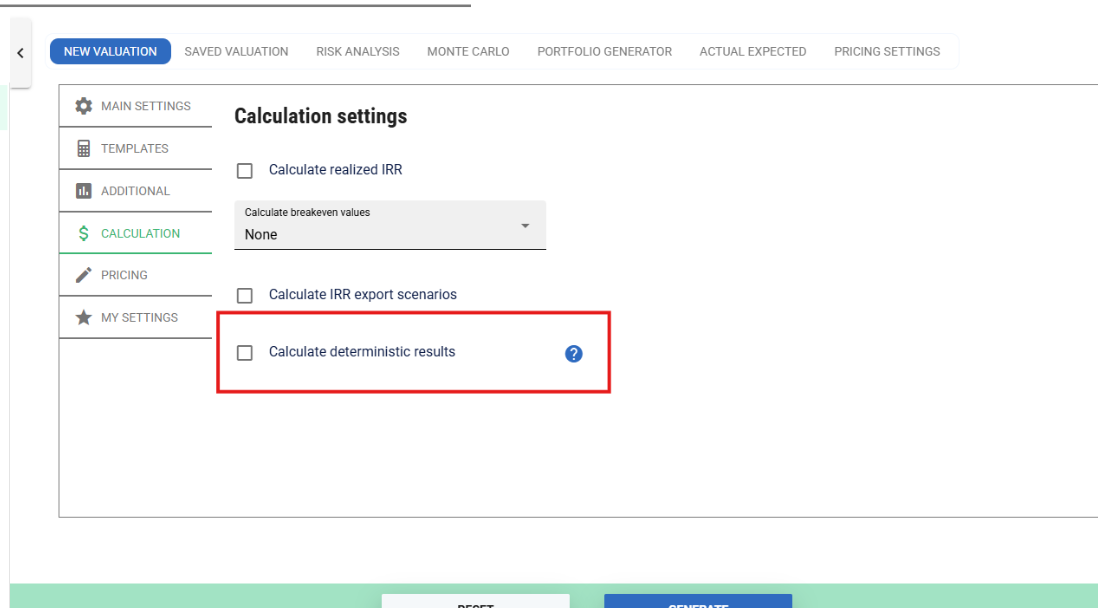
Calculate Deterministic Results
The Portfolio Valuation model includes the option to calculate some deterministic values in addition to the standard probabilistic output. This is selected by checking the box highlighted below. This adds a further option to the downloads under Detailed Results:
The Excel sheet which is generated from this link contains the following data points for each Case in the Portfolio:
| Column Name | Description |
|---|---|
| Index | Starting at 1. |
| Case Reference | The ClariNet LS Case Reference. |
| NDB | The Face Amount of the policy. |
| Policy Type | Taken from the Policy Type field. |
| Purchase Date | The policy Purchase Date, taken from the Cost/Maturity/Disposal tab. |
| Purchase Cost | The policy Purchase Cost, taken from the Cost/Maturity/Disposal tab. |
| Value Date | The portfolio valuation Value Date. |
| Used LE | The blended Mean LE50, calculated from the blended underwriting date. |
| Aged LE | The Mean LE50 calculated from Value Date. |
| Implied Mortality | The implied mortality factor. |
| Joint Life | Y/N depending on policy type. |
| Scenario X NPV | The policy NPVs, calculated from the parameters specified on the valuation screen. |
| LE Date Fields | |
| LE Date | This date is calculated by taking the Aged Mean LE50 on Value Date and adding that number of months to Value Date. The number of months is rounded down. |
| Insured X Age | The age of the insured on the LE Date, calculated using ALB. |
| Cost Basis | NDB – Premiums – Purchase Costs. |
| Total Premiums | The sum of the premiums from Purchase Date until LE Date. Premiums prior to Value Date are taken from Premium History. Premiums on or after Value Date are taken from the Pricing Premium Schedule. |
| Surv Prob | The survival probability calculated at LE Date. |
| IRR | The IRR, calculated by discounting cashflows back to Purchase Date, such that they are equal to total Purchase Cost. These cashflows include the NDB and the Premiums (as specified above). |
| Breakeven Date Fields | |
| Breakeven Date | The date at which the Cost Basis (as defined above) is zero, i.e., Purchase Costs plus Premiums equals NDB. |
| Insured X Age | The age of the insured on Breakeven Date, calculated using ALB. |
| Cost Basis | NDB – Premiums – Purchase Costs |
| Total Premiums | The sum of the premiums from Purchase Date until Breakeven Date. Premiums prior to Value Date are taken from Premium History. Premiums on or after Value Date are taken from the Pricing Premium Schedule. |
| Surv Prob | The survival probability calculated at Breakeven Date. |
| IRR | This value should be close to 0%. |
| Coverage End Date Fields | |
| Coverage End Date | The date at which policy coverage ends. |
| Coverage End Age | Taken from the Policy Maturity Age plus the DB Rider (if appropriate). |
| Insured X Age | The age of the insured on Coverage End Date, calculated using ALB. |
| Cost Basis | NDB – Premiums – Purchase Costs. |
| Total Premiums | The sum of the premiums from Purchase Date until Coverage End Date. Premiums prior to Value Date are taken from Premium History. Premiums on or after Value Date are taken from the Pricing Premium Schedule. |
| Surv Prob | The survival probability calculated at Coverage End Date. |
| IRR | The IRR, calculated by discounting cashflows back to Purchase Date, such that they are equal to total Purchase Cost. These cashflows include the NDB and the Premiums (as specified above). |
| Comments |
Single Policy Deterministic Pricing
The single policy pricing page includes deterministic results in this tab:
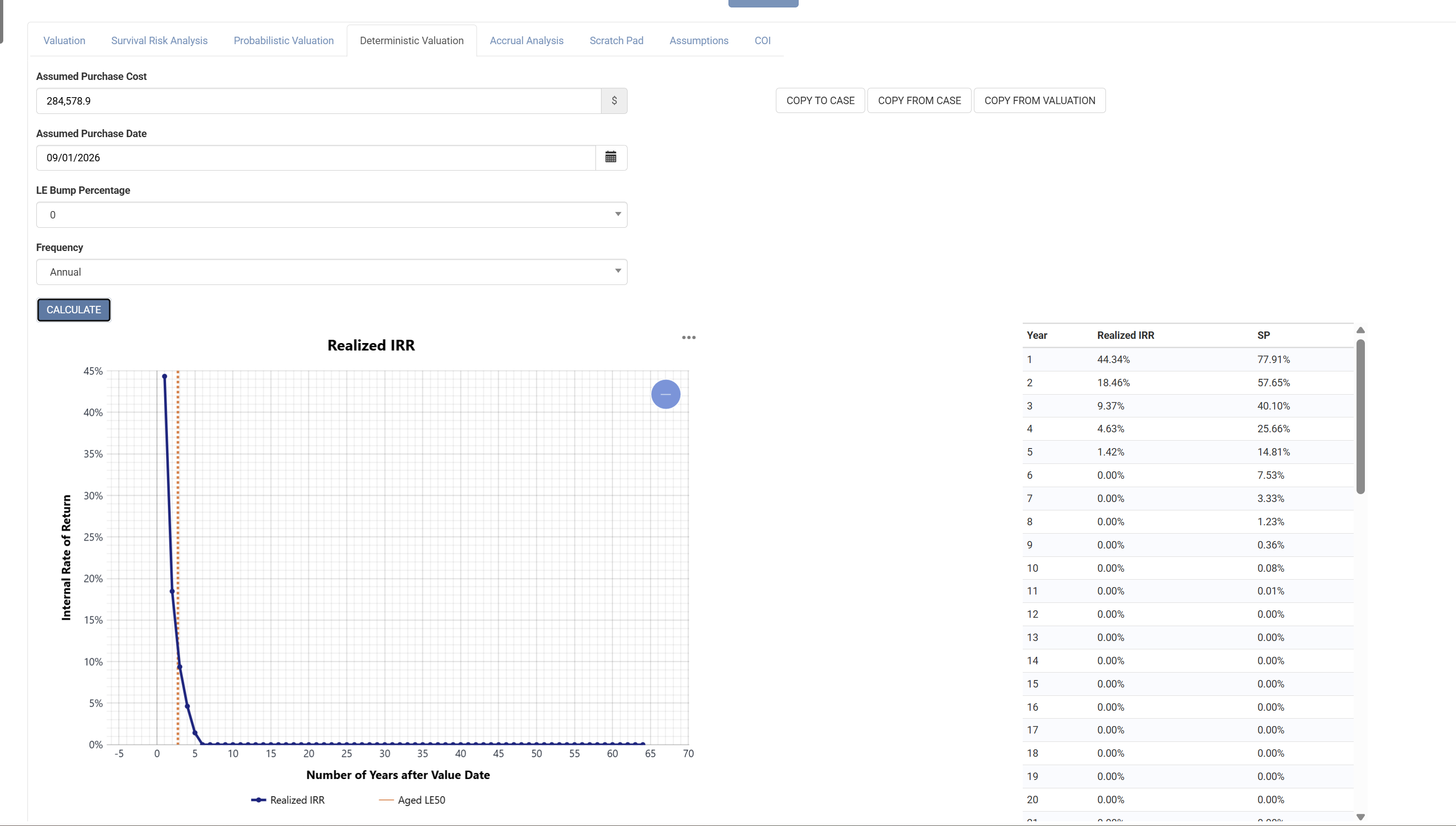
The results are similar to the portfolio deterministic pricer. The key differences are:
- The calculations are all relative to the Assumed Purchase Date;
- The Aged Mean LE50 used for the result "LE 50 Plus Bump X%" is calculated on Assumed Purchase Date (note that the bump percentage is specified above);
